138 - 62 不同路径

题目

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

img

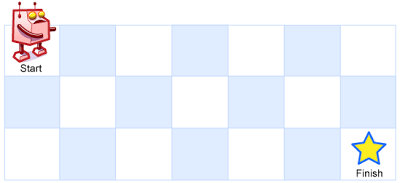
例如，上图是一个7 x 3 的网格。有多少可能的路径？

说明：m 和 n 的值均不超过 100。

示例 1:

输入: m = 3, n = 2 输出: 3 解释: 从左上角开始，总共有 3 条路径可以到达右下角。

1. 向右 -> 向右 -> 向下

2. 向右 -> 向下 -> 向右

3. 向下 -> 向右 -> 向右

示例 2:

输入: m = 7, n = 3 输出: 28

解答

感觉就是动态规划的题dp[i][j] = dp[i-1][j] + dp[i][j-1]

然后第一行和第一列都是1

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        ans = [[1]*n] + [[1]+[0] * (n-1) for _ in range(m-1)]
        for i in range(1, m):
            for j in range(1, n):
                ans[i][j] = ans[i-1][j]+ans[i][j-1]
        return ans[m-1][n-1]

Runtime: 28 ms, faster than 98.61% of Python3 online submissions for Unique Paths.

Memory Usage: 12.7 MB, less than 100.00% of Python3 online submissions for Unique Paths.

但是最后生成的这个矩阵是对称矩阵，也就是说只需要算一半就行了

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        cur = [1] * n
        for _ in range(1, m):
            for j in range(1, n):
                cur[j] += cur[j-1]
                print("cur", cur)
        return cur[-1]

Runtime: 32 ms, faster than 93.07% of Python3 online submissions for Unique Paths.

Memory Usage: 12.7 MB, less than 100.00% of Python3 online submissions for Unique Paths.

反而变慢了哈哈😂

var uniquePaths = function(m, n) {
  let cur = new Array(n)
  for (let i = 0; i < n; i++) {
    cur[i] = 1
  }
  for (let i = 1; i < m; i++) {
    for (let j = 1; j < n; j++) {
      cur[j] += cur[j - 1]
    }
  }
  return cur[cur.length - 1]
};

Runtime: 60 ms, faster than 39.27% of JavaScript online submissions for Unique Paths.

Memory Usage: 34.1 MB, less than 54.55% of JavaScript online submissions for Unique Paths.

func uniquePaths(m int, n int) int {
    cur := make([]int, n)
    for i := 0; i < n; i++ {
        cur[i] = 1
    }
    for i := 1; i < m; i++ {
        for j := 1; j < n; j++ {
            cur[j] += cur[j-1]
        }
    }
    return cur[len(cur)-1]
}

Runtime: 0 ms, faster than 100.00% of Go online submissions for Unique Paths.

Memory Usage: 2 MB, less than 100.00% of Go online submissions for Unique Paths.