165 - 887 鸡蛋掉落
题目
你将获得 K 个鸡蛋，并可以使用一栋从 1 到 N 共有 N 层楼的建筑。
每个蛋的功能都是一样的，如果一个蛋碎了，你就不能再把它掉下去。
你知道存在楼层 F ，满足 0 <= F <= N 任何从高于 F 的楼层落下的鸡蛋都会碎，从 F 楼层或比它低的楼层落下的鸡蛋都不会破。
每次移动，你可以取一个鸡蛋（如果你有完整的鸡蛋）并把它从任一楼层 X 扔下（满足 1 <= X <= N）。
你的目标是确切地知道 F 的值是多少。
无论 F 的初始值如何，你确定 F 的值的最小移动次数是多少？
示例 1：
输入：K = 1, N = 2 输出：2 解释： 鸡蛋从 1 楼掉落。如果它碎了，我们肯定知道 F = 0 。 否则，鸡蛋从 2 楼掉落。如果它碎了，我们肯定知道 F = 1 。 如果它没碎，那么我们肯定知道 F = 2 。 因此，在最坏的情况下我们需要移动 2 次以确定 F 是多少。
示例 2：
输入：K = 2, N = 6 输出：3
示例 3：
输入：K = 3, N = 14 输出：4
提示：
1 <= K <= 100
1 <= N <= 10000
解答
对这个大佬文章的整理：
题目中的要点：
找一个f楼，f楼扔鸡蛋不会碎，f+1楼扔鸡蛋会碎。f可以等于0
最坏情况，需要扔几次？
最坏情况，意味着鸡蛋破碎一定在搜索区间穷尽的时候。
鸡蛋可以复用，比如7层楼，5楼碎，那么一个鸡蛋，可以从1楼开始试到4楼。
换言之从下往上一层层楼试，总能试出是第几层的。不过问题是要求最优解
动态规划
状态：
当前拥有的鸡蛋数
K和需要测试的楼层数N由于只需要知道，最多试几次能试出来，因此具体几楼到几楼，这些信息可以忽视
选择：
这一轮，去哪一层楼扔鸡蛋
因此要有一个for循环，这一轮扔哪层不知道，就一个个去试
状态转移：
在第
i层扔鸡蛋。如果鸡蛋碎了，那么搜索楼层变成
[1,i-1]，i-1层如果鸡蛋没碎，那么搜索楼层变成
[i+1,n]，N-i层
base case：
如果只有一个鸡蛋
k=1，那么只能从下往上一层层尝试，即扔n次如果n=0，即不需要扔鸡蛋
暴力解
class Solution:
def superEggDrop(self, K: int, N: int) -> int:
def dp(k, n):
if k == 1: # 只有一个鸡蛋，遍历
return n
if n == 0: # 没有楼层，不用扔
return 0
res = n # 最坏情况就是一层层楼扔
for i in range(1, n+1): # 本轮，在第1层到n层 之间，选一个扔
res = min(res, # 现有结果
max( # 最坏情况
dp(k-1, i-1), # 扔碎了，需要搜索的楼层变成了i-1层
dp(k, n-i) # 没扔碎，搜索楼层变成n-i层
)+1 # 本轮已经花费了一次尝试
)
return res
return dp(K, N)显然超时
备忘录优化
class Solution:
def superEggDrop(self, K: int, N: int) -> int:
memo = {}
def dp(k, n):
if k == 1:
return n
if n == 0:
return 0
if (k, n) in memo:
return memo[(k, n)]
res = n
for i in range(1, n+1):
res = min(res, max(dp(k-1, i-1), dp(k, n-i))+1)
memo[(k, n)] = res
return res
return dp(K, N)结果也超时了。。。
var superEggDrop = function(K, N) {
const memo = {}
const dp = function(k, n) {
key = k + "," + n
if (key in memo) {
return memo[key]
}
if (k === 1) {
return n
}
if (n === 0) {
return 0
}
let res = n
for (let i = 1; i < n + 1; i++) {
res = Math.min(res, 1 + Math.max(dp(k - 1, i - 1), dp(k, n - i)))
}
memo[key] = res
return res
}
return dp(K, N)
};js也超时了。
二分搜索优化
楼层增加，需要测算的次数一定也会跟着增加。具体到dp这个函数，当n增加，结果一定也是线性增加的。
同样，楼层减少，需要测算次数也是线性减少的。
所以求Math.max(dp(k - 1, i - 1), dp(k, n - i))，也就是求一点，使得dp(k-1,i-1)==dp(k,n-i)
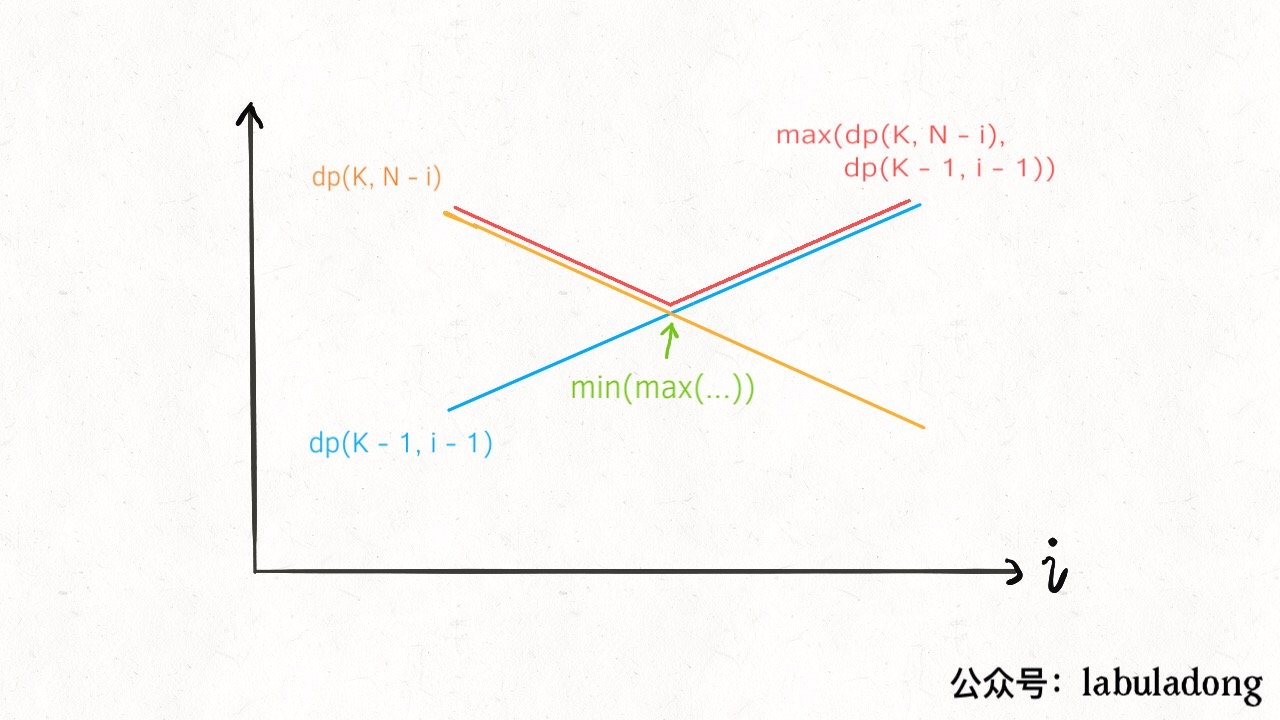
因此我们需要优化其中的搜索部分，不再是从1到n，而是用二分搜索
class Solution:
def superEggDrop(self, K: int, N: int) -> int:
memo = {}
def dp(k, n):
if (k, n) in memo:
return memo[(k, n)]
if k == 1:
return n
if n == 0:
return 0
res = n
left, right = 1, n
while left < right:
mid = (left+right) >> 1
broken = dp(k-1, mid-1)
unBroken = dp(k, n-mid)
if broken > unBroken:
right = mid
res = min(res, broken+1)
else:
left = mid+1
res = min(res, unBroken+1)
memo[(k, n)] = res
return res
return dp(K, N)Runtime: 2584 ms, faster than 13.26% of Python3 online submissions for Super Egg Drop.
Memory Usage: 42.4 MB, less than 11.11% of Python3 online submissions for Super Egg Drop.
巨慢。。。
状态转移优化
class Solution:
def superEggDrop(self, K: int, N: int) -> int:
dp = [[0]*(N+1)]*(K+1)
m = 0
while dp[K][m] < N:
m += 1
for k in range(1, K+1):
dp[k][m] = dp[k][m-1]+dp[k-1][m-1]+1
return mvar superEggDrop = function(K, N) {
const dp = new Array(K + 1)
for (let i = 0; i < K + 1; i++) {
dp[i] = new Array(N + 1)
for (let j = 0; j < N + 1; j++) {
dp[i][j] = 0
}
}
let m = 0
while (dp[K][m] < N) {
m++
for (let k = 1; k < K + 1; k++) {
dp[k][m] = dp[k][m - 1] + dp[k - 1][m - 1] + 1
}
}
return m
};Runtime: 124 ms, faster than 25.00% of JavaScript online submissions for Super Egg Drop.
Memory Usage: 57 MB, less than 100.00% of JavaScript online submissions for Super Egg Drop.
Last updated
Was this helpful?