187 - 295 数据流的中位数

题目

中位数是有序列表中间的数。如果列表长度是偶数，中位数则是中间两个数的平均值。

例如，

[2,3,4] 的中位数是 3

[2,3] 的中位数是 (2 + 3) / 2 = 2.5

设计一个支持以下两种操作的数据结构：

• void addNum(int num) - 从数据流中添加一个整数到数据结构中。

• double findMedian() - 返回目前所有元素的中位数。

示例：

addNum(1) addNum(2) findMedian() -> 1.5 addNum(3) findMedian() -> 2

进阶:

• 如果数据流中所有整数都在 0 到 100 范围内，你将如何优化你的算法？

• 如果数据流中 99% 的整数都在 0 到 100 范围内，你将如何优化你的算法？

解答

暴力法

一开始只能想到，翻译一下题目的做法：

class MedianFinder:

    def __init__(self):
        """
        initialize your data structure here.
        """
        self.data = []

    def addNum(self, num: int) -> None:
        self.data.append(num)
        self.data.sort()

    def findMedian(self) -> float:
        size = len(self.data)
        if (size & 1) == 0:
            # 偶数
            return (self.data[size//2]+self.data[size//2-1])/2
        else:
            # 奇数
            return self.data[size//2]

Runtime: 1252 ms, faster than 6.40% of Python3 online submissions for Find Median from Data Stream.

Memory Usage: 24.2 MB, less than 6.67% of Python3 online submissions for Find Median from Data Stream.

令我没想到的是，居然还有人能比我还慢哈哈😂

https://leetcode-cn.com/problems/find-median-from-data-stream/solution/shu-ju-liu-de-zhong-wei-shu-by-leetcode/

看题解发现，还能用插入排序，即插入的时候，二分法找到插入的地方，然后插入。

大小顶堆

https://leetcode-cn.com/problems/find-median-from-data-stream/solution/you-xian-dui-lie-python-dai-ma-java-dai-ma-by-liwe/

https://leetcode.com/problems/find-median-from-data-stream/discuss/74062/Short-simple-JavaC%2B%2BPython-O(log-n)-%2B-O(1)

因为我们只要中位数的信息，完全没必要排序其他的数。

因此可以把数组分成两半，小的一半用大顶堆，留出最大数；大的一半用小顶堆，留出最小数。

直接拿liweiwei大佬的题解图了：

img

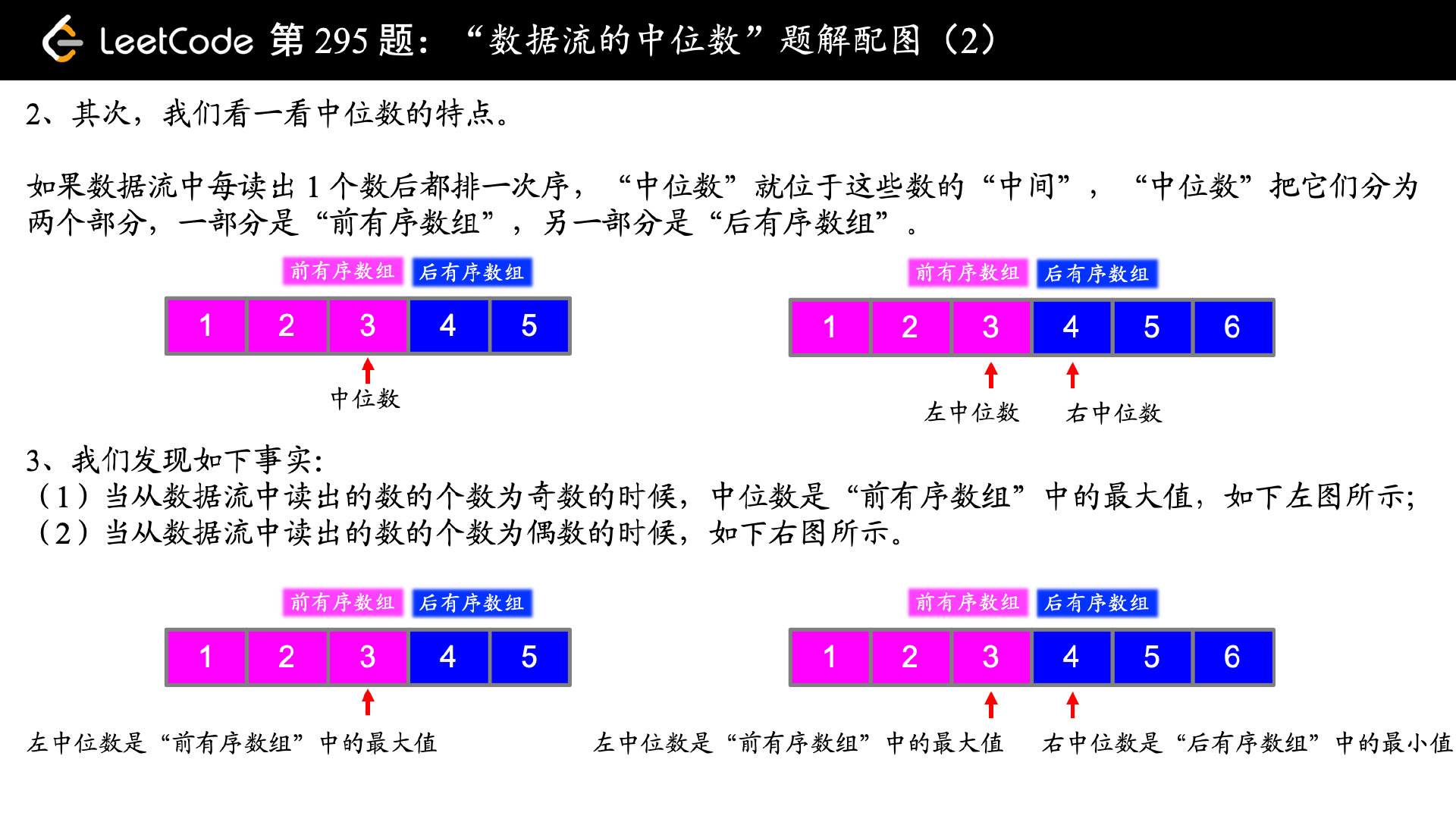
这样获取了中间的两个值。我们只要保证，小的那一半，比大的那一半，多一个数，就行了。

from heapq import *
class MedianFinder:

    def __init__(self):
        """
        initialize your data structure here.
        """
        self.heap = [], []

    def addNum(self, num: int) -> None:
        small, large = self.heap
        heappush(small, -heappushpop(large, num))
        if len(large) < len(small):
            heappush(large, -heappop(small))

    def findMedian(self) -> float:
        small, large = self.heap
        if len(large) > len(small):
            return float(large[0])
        return (large[0]-small[0])/2.0

Runtime: 188 ms, faster than 93.20% of Python3 online submissions for Find Median from Data Stream.

Memory Usage: 23.9 MB, less than 13.33% of Python3 online submissions for Find Median from Data Stream.